Initially, values of all memory cells and gates are set to X’s. The application binary is loaded into program memory, providing values that effectively constrain which gates can be toggled during execution. During simulation, the simulator sets all inputs to X’s, which propagate through the gate-level netlist during simulation.
After each cycle is simulated, toggled gates are removed from the list of unexercisable gates. Gates where an ‘X’ propagated are considered as toggled, since some input assignment could cause the gates to toggle. If an ‘X’ propagates to the PC, indicating input-dependent control flow, the simulator branches the execution tree and simulates execution for all possible branch paths, following depth-first ordering of the control flow graph.
This naive simulation approach does not scale well for complex or infinite control structures which result in a large number of branches to explore. So a conservative approximation could be employed that allows the analysis to scale for arbitrarily-complex control structures while conservatively maintaining correctness in identifying exercisable gates. The approximation works by tracking the most conservative gate-level state that has been observed for each PC-changing instruction. The most conservative state is the one where the most variables are assumed to be unknown (X).
When a branch is re-encountered while simulating on a control flow path, simulation down that path can be terminated if the symbolic state being simulated is a sub-state of the most conservative state previously observed at the branch, since the state (or a more conservative version) has already been explored. If the simulated state is not a sub-state of the most conservative observed state, the two states are merged to create a new conservative symbolic state by replacing differing state variables with X’s, and simulation continues from the conservative state. This conservative approximation technique allows gate activity analysis to complete in a small number of passes through the application code, even for applications with an exponentially-large or infinite number of execution paths.
The result of input-independent gate activity analysis for an application is a list of all gates that cannot be toggled in any execution of the application, along with their constant values. Since the logic functions performed by these gates are not necessary for the correct execution of the binary for any input, these may safely be cut from the netlist as long as their constant output values are preserved. The following section describes how unusable gates can be cut from the processor without affecting its functionality for the target application.
Cutting and stitching
Once gates that the target application cannot toggle are identified, these are cut from the processor netlist for the bespoke design. After cutting out a gate, the netlist must be stitched back together to generate the final netlist and laid-out design for the bespoke processor.
Fig. 5 shows the method for cutting and stitching a bespoke processor. First, each gate on the list of unusable gates is removed from the gate-level netlist. After removing a gate, all fan-out locations that were connected to its output net are tied to a static voltage (‘1’ or ‘0’) corresponding to the constant output value of the gate observed during simulation. Since logical structure of the netlist has changed, the netlist is re-synthesised after cutting all unusable gates to allow additional optimisations that reduce area and power.
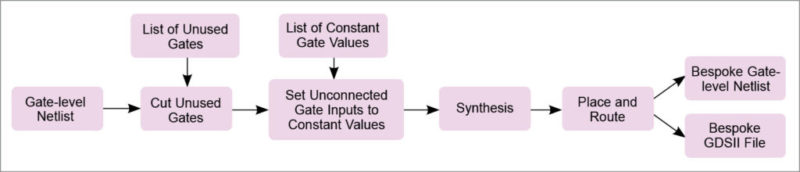
Gates having constant inputs after cutting and stitching can be replaced with simpler gates. Also, toggled gates left with floating outputs after cutting can be removed, as their outputs can never propagate to a state element or output port. Since cutting can reduce the depth of logic paths, some paths may have extra timing slack after cutting, allowing faster, higher-power cells to be replaced with smaller, lower-power versions of the cells. Finally, the re-synthesised netlist is placed and routed to produce the bespoke processor layout, as well as a final gate-level netlist with necessary buffers, etc to meet timing constraints.












